Y seguimos

Les vuelvo a aclarar que el hecho de que explique todos estos términos tan "ñoños" que para algunos sean desconocidos, son para entender mejor el mundo microscópico.
Bueno como les iba diciendo, esta ecuación de Schorodinger tiene como función encontrar la forma matemática a través de la cuál pueda determinarse el comportamiento de las partículas en escala diminuta. El detalle se encuentra en que esta ecuación no determina el comportamiento exacto, es decir, las velocidades, posiciones, trayectorias, etc. de una partícula en esta escala, son sólo aproximadas.
Esta ecuación, también conocida como ecuación de onda, establece distintos aspectos:

• La existencia de un núcleo atómico.
• Los niveles energéticos donde se pueden encontrar los electrones en base a su energía.
• La dualidad onda-partícula.
• La probabilidad de encontrar al electrón con respecto al tiempo (algo que hasta el momento no se a logrado un 100% por ciento)

Tampoco me adentraré demasiado en este tema ya que existen muchos términos y conceptos que tampoco conosco y que ni entiendo, pero también se relacionan otros muy conocidos como la energía cinética o la energía potencial. En esta ecuación se describe una partícula con energía E relacionada con términos como la cantidad de movimiento(p), la longitud de onda, la frecuencia(v), de la siguiente manera:

E= p^2 / 2m + V ( r )

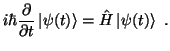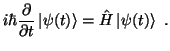La solución de esta fórmula, da como resultado la función de onda, es decir, una forma probabilística de hallar un electrón en un determinado espacio, conocido cómo orbital. Y existen otras maneras de expresar esta ecuación como  pero a mi parecer nos quedamos con la otra, es un poquito más sencillita, ¿No creen?

Pero como les he comentado, esta ecuación así como otras que también estudiaremos, son aproximaciones del comportamiento, es decir, la mecánica cuántica tiene una manera de estudio muy diferente a la mecánica clásica ya que la MC se basa en las incertidumbres...